Lépjünk vissza egy lépést a Dirac-deltától...

 

1(t) egységugrás

 

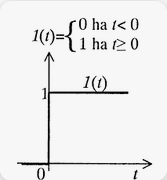
Tegyük fel, hogy t=0 időpillanatban f(t)=1=(t) bemenő jelet kapcsolunk egy RC osztóra.

A válasz a kimeneten: g(t) = 1-exp(-t/RC) lesz. (A kép csak illusztráció.)

Ezt elfogadhatjuk a priori tapasztalatnak. Az okozat nem előzi meg az okot.

 

Mi történik, ha ezt az egységugrást kikapcsoljuk egy későbbi időpontban?

Lineáris szuperpozíció.

Bemenet: f(t) = 1(t-t₁) - 1(t-t₂)

Ahogyan a kimeneten is össze kell adini az "elemi" válaszfüggvényeket: g(t-t₁)-g(t-t₂)

 

Teljes indukcióval beláthatjuk, hogy egy tetszőleges f(t) függvényt jól közelíthetünk ilyen lépcsőkre bontással.

 

f(t) = f(t_i) ∑ ∆f_i

Ez még csak differencia. Nem differencia hányados.

Nem találtam jobb képet. Lépcsőket kellett volna berajzolni.

 

És most jön a ravasz kérdés, amit annak idején bemondásra hittünk el. (Bizonyítani kellene.)

Veszünk egy periodikus jelet. Ez minden pillanatban elindít egy új tranziens választ, amely a korábbiakhoz szuperponálódik (konvolúció). Az állítás az, hogy néhány időállandóval később egy állandósult válasz fog jönni, vagyis a tranziens akkor is megszűnik, ha a bemenetre periodikusan változó jel kerül.

(Matematikából sem magyarázták, hogy a differenciál partikuláris megoldását miért lehet hozzáadni az általános megoldáshoz. Szabály és "darálunk" vele.)

 

Összefoglalás:

1. Elfogadjuk elsődleges tapasztalatnak, hogy válasz csak a kérdés után jön. Kauzalitás.

2. Egymás után több ok miatt az okozatok szuperpozícióját tapasztaljuk.

3. Valahogy meg kellene mutatni, hogy a periodikus bemenő jelre a konvolúció egy fázistoláshoz tart.