"Attól, hogy a rádióhullám amplitúdója felfut, majd lecseng, miért lenne benne több frekvenciakomponens?"

 

Ezt teszi a Fourier-transzformáció.

 

Viszont... álmodtam valamit.

Már pontosan nem emlékszem.

De az értelme az volt, hogy a negatív frekvenciákat nem kellene figyelembe venni.

 

 

 

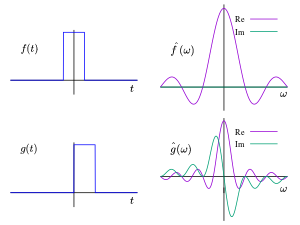
https://en.wikipedia.org/wiki/Fourier_transform#Negative_frequency

For real-valued functions, there is a simple relationship between the values of the Fourier transform for positive and negative ξ (see conjugation below). This makes it possible to avoid the subject of negative frequencies by using the sine and cosine transforms. But most authors prefer using Eq.1 rather than using two transforms. One reason for this is that many applications have to take the Fourier transform of complex-valued functions, such as partial differential equations, radar, nonlinear optics, quantum mechanics, and others. In these cases, the value of the Fourier transform at negative frequencies is distinct from the value at real frequencies, and they are important. In these situations, the concept of what is a frequency is defined by the Fourier transform rather than appealing to a rate or period.

 

De a lényeg nem is ez, hanem az inverze.

Mert például a jelenre - éppen a kauzalitás miatt - csak a múltbéli eseményeknek lehet hatásuk, a jövőbelieknek nem.

Illetve a jelen kezdeti állapotnak a jövőben lehet következménye, de a múltban kizárt.

Ezért inkább vagy csak a pozitív időfélsíkon, vagy csak a negatív időfélsíkon kellene integrálni.

 

A probléma a szócikk szerint ott van, hogy ugyebár a komplex értékű függvényekkel ez nem megy.

Na de hol vannak komplex függvények?

A mérhető fizikai mennyiségek valósak.

Csak számítási segédlet a komplex függvénytan.