Kételkedek...

 

∇A = ∂_xA_x + ∂_yA_y + ∂_zA_z

∇B = ∂_xB_x + ∂_yB_y + ∂_zB_z

Mindkettő skalár.

 

Ezt megszorozva egy vektorral:

A(∇B) = i A_x ∙ (∂_xB_x + ∂_yB_y + ∂_zB_z) + j A_y ∙ (∂_xB_x + ∂_yB_y + ∂_zB_z) + k A_z ∙ (∂_xB_x + ∂_yB_y + ∂_zB_z)

B(∇A) = i B_x ∙ (∂_xA_x + ∂_yA_y + ∂_zA_z) + j B_y ∙ (∂_xA_x + ∂_yA_y + ∂_zA_z) + k B_z ∙ (∂_xA_x + ∂_yA_y + ∂_zA_z)

 

Jelent valamit a skaláris szorzás zárójelezése?

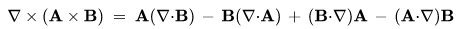
Most először számoljuk ki, ha a differenciál operátort balról skalárisan szorozzuk:

A∇ = ∂_xA_x + ∂_yA_y + ∂_zA_z

B∇ = ∂_xB_x + ∂_yB_y + ∂_zB_z

Szerintem ez ugyanaz, mint fent.

Ez már nem tud operátorként hatni.

 

(A∇)B = (∂_xA_x + ∂_yA_y + ∂_zA_z) ∙ (i B_x+j B_y+k B_z)

(B∇)A = (∂_xB_x + ∂_yB_y + ∂_zB_z) ∙ (i A_x+j A_y+k A_z)

 

(A∇)B = i B_x ∙ (∂_xA_x+∂_yA_y+∂_zA_z) + j B_y ∙ (∂_xA_x+∂_yA_y+∂_zA_z) + k B_z ∙ (∂_xA_x+∂_yA_y+∂_zA_z)

(B∇)A = i A_x ∙ (∂_xB_x+∂_yB_y+∂_zB_z) + j A_y ∙ (∂_xB_x+∂_yB_y+∂_zB_z) + k A_z ∙ (∂_xB_x+∂_yB_y+∂_zB_z)

 

 

Hasonlítsuk össze:

A(∇B) = i A_x ∙ (∂_xB_x+∂_yB_y+∂_zB_z) + j A_y ∙ (∂_xB_x+∂_yB_y+∂_zB_z) + k A_z ∙ (∂_xB_x+∂_yB_y+∂_zB_z)

(B∇)A = i A_x ∙ (∂_xB_x+∂_yB_y+∂_zB_z) + j A_y ∙ (∂_xB_x+∂_yB_y+∂_zB_z) + k A_z ∙ (∂_xB_x+∂_yB_y+∂_zB_z)

 

B(∇A) = i B_x ∙ (∂_xA_x+∂_yA_y+∂_zA_z) + j B_y ∙ (∂_xA_x+∂_yA_y+∂_zA_z) + k B_z ∙ (∂_xA_x+∂_yA_y+∂_zA_z)

(A∇)B = i B_x ∙ (∂_xA_x+∂_yA_y+∂_zA_z) + j B_y ∙ (∂_xA_x+∂_yA_y+∂_zA_z) + k B_z ∙ (∂_xA_x+∂_yA_y+∂_zA_z)

 

A zárójelezés megfordítja a sorrendet, ahogy ez várható volt.

Vagyis a kétszeresét kell venni az első két tagnak. Az utolsó két tag ugyanaz.